Question

a six-sided number cube is rolld twice, what is the probability that the first cough will be less than 4 and the second coughs withh be a number greater than 4?

Answer 1

Not sure what you mean by "cough". I assume you mean the number on the face.

The rolls are independent, so


`\mathbb P(\text{first roll < 4 AND second roll > 4})=\mathbb P(\text{first roll < 4})\cdot\mathbb P(\text{second roll > 4})`

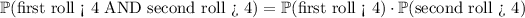
For the first roll, there are three ways of getting a number less than 4 (1, 2, or 3) with a probability of
`\frac36=\frac12`.

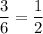
For the second roll, there are two ways of getting a number greater than 4 (5 or 6) with a probability of
`\frac26=\frac13`.

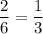
So the probability of both events occurring in the prescribed order is
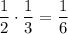
`\frac12\cdot\frac13=\frac16`.