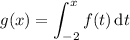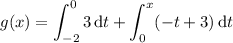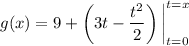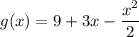Question

CALCULUS HELP AGAIN PLS HELP ME GRADUATE

Answer 1

1. Using the trapezoidal rule, you get


`\displaystyle\int_0^8R(t)\,\mathrm dt\approx\frac{2.5+1.95}2(2-0)+\frac{2.8+2.5}2(3-2)+\frac{4+2.8}2(7-3)+\frac{4.26+4}2(8-7)`

`\displaystyle\int_0^8R(t)\,\mathrm dt\approx24.830\text{ gal}`


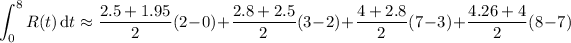
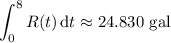
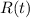
`R(t)` gives the rate at which the water flows, so if you integrate with respect to time, you get the actual amount of water. In the summation above, the differences between successive
`t`'s form the heights of the trapezoids, while the successive values of
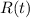
`R(t)` form the "bases" of the trapezoids for which you take the averages.

2. Possibly... We know that
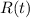
`R(t)` is differentiable, so
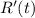
`R'(t)` certainly exists and must be continuous. The intermediate value theorem says that, on the interval
`[0,8]`, we can find some
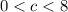
`0<c<8` such that
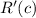
`R'(c)` would fall between
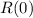
`R(0)` and
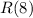
`R(8)`. But from the given data, we can't guarantee that
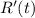
`R'(t)` is ever 0, because both
`R(0)=1.95` and
`R(8)=4.26`.

3. The average rate of water flow would be


`R_\text{average}=(W(8)-W(0))/(8-0)=\frac{\ln71-\ln7}8\approx0.290\text{ gal/hr}`

4.
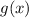
`g(x)` is increasing whenever
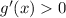
`g'(x)>0`. By the fundamental theorem of calculus,


`g'(x)=(\mathrm d)/(\mathrm dx)\displaystyle\int_(-2)^xf(t)\,\mathrm dt=f(x)`

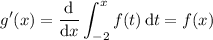
and
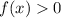
`f(x)>0` for
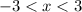
`-3<x<3` only.

5. For
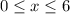
`0\le x\le6`, we have
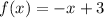
`f(x)=-x+3`, so


`g(x)=\displaystyle\int_(-2)^xf(t)\,\mathrm dt`

`g(x)=\displaystyle\int_(-2)^03\,\mathrm dt+\int_0^x(-t+3)\,\mathrm dt`

`g(x)=9+\left(3t-\frac{t^2}2\right)\bigg|_(t=0)^(t=x)`

`g(x)=9+3x-\frac{x^2}2`