Answer: Second option :
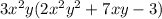
Explanation:
Given expression
 .
.
We need to find greatest common factor (GCF) of all the terms.
Let us write all terms in expanded form first.
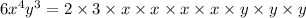
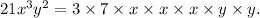
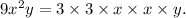
We can see that first factor is 3 common, second factor is
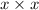 and third factor is y.
and third factor is y.
Therefore, GCF would be
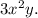
Now, let us factor out GCF
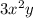 and keep the remaining terms inside parenthesis.
and keep the remaining terms inside parenthesis.
=
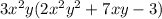
Therefore, correct option is 2nd option
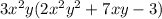 .
.