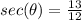Answer:
(1)
b.
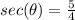
(2)
b.
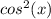
(3)
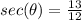
Explanation:
(1)
we are given
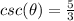
we can use triangle method
we know that
csc=hyp/ opposite
so, hyp=5
opposite =3
now, we can find adjacent
we can use Pythagoras theorem
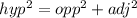
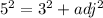
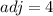
now, we can find sec
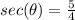
(2)
we are given
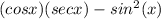
we can simplify it
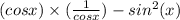
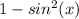
now, we can replace 1 as sin^2x +cos^2x
we get
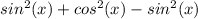
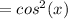
(3)
we are given
θ is in Quadrant IV
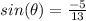
we know that
sin =opp/hyp
so, opp=5
hyp=13
now, we can use Pythagoras theorem
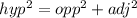
now, we can plug values
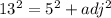
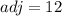
sec=hyp/adj
so, we get