Question

Which function is an odd function?

Answer 1

B: f(x)=csc(-3pi/2x)

Explanation:

Got it correct.

Answer 2

For any trigonometric point P(x,y)

x always represents cos

`x=cos\theta`

y always represents sin.

`y=sin\theta`

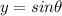
Now if we drop a perpendicular from P(x,y) to a point Q which is a refelction of P across x axis, we get Q(x, -y) for the same angle.

The angle shall be
`-\theta`

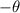
So now

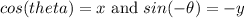`cos(\-theta)=x $ and $ sin(-\theta) = -y` ...(1)

But
`x=cos\theta $ and $ y = sin\theta`

Statement (1) becomes

`cos(-\theta) = cos\theta $ and $ sin(-\theta) = -sin\theta`

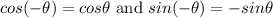
So the value of cos does not change, but the value of sin changes.

Cos is even & sin is odd.

And so sec is even and cosec is odd.

So
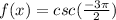`f(x) = csc((-3\pi)/(2))` shall be an odd function.

Option B) is the right answer