Question

What is the length of line segment EF? Enter your answer, as a decimal rounded to the nearest tenth, in the box.

Answer 1

2^2 + 3^2 = 4 + 9 = 13
EF = √13 = 3.6

answer
3.6

Answer 2

3.6 units.

Explanation:

We have been given an image of a coordinate plane. We are asked to find the length of line segment EF.

We will use distance formula to solve our given problem.

`\text{Distance}=√((x_2-x_1)^2+(y_2-y_1)^2)`

Upon substituting our given values in above formula we will get,

`\text{Distance}=√((-1--3)^2+(-2-1)^2)`

`\text{Distance}=√((-1+3)^2+(-3)^2)`

`\text{Distance}=√((2)^2+(-3)^2)`

`\text{Distance}=√(4+9)`

`\text{Distance}=√(13)`

`\text{Distance}=3.60555\approx 3.6`

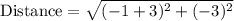
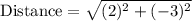
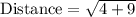
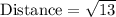
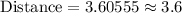
Therefore, the length of line segment EF is 3.6 units.