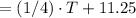Question

A dump truck weighs 11.25 tons when empty a conveyor belt pours sand into the truck at a constant rate of 1/4 ton per minute until it's full. let T represent the elapsed time in minutes. Let W represent the weight of the truck after T minutes.

Write an equation for W in terms if T

W(T)=________

Answer 1

W(T)
`=(1/4)\cdot{T}+11.25`

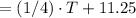
Explanation:

The orignial weight of the truck is 11.25 and this remains a constant weight of the truck throughoout the loading of the sand. If the expression is written in terms of weight, we must convert the mass flow (ton/min) to weight in tons. This can be done by multiplying with time T minutes. The total weight after T minutes is the sum of the weight of the truck and the sand:

W(x)
`=(1/4)\cdot{x}+11.25`

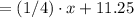
W(T)
`=(1/4)\cdot{T}+11.25`

Answer 2

For this case, the first thing we must do is define variables.
We have then:
t: time in minutes
The linear equation that represents the problem is given by:
w (t) = (1/4) t + 11.25
Answer:
An equation for W in terms if T is:
w (t) = (1/4) t + 11.25