Question

A 2,000 g quantity of C-14 is left to undergo radioactive decay. The half-life of C-14 is approximately 5,700 years. After going trough x half-lives, the sample becomes 125 grams. What is x? A) 22,800 B) 28,500 C) 4 D) 5

Answer 1

The half-life is the time the sample takes to reduce to half of its original value. If we call
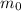
`m_0` the initial mass of the sample, this means that after 1 half-life the mass will be
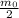
`(m_0)/(2)`, after 2 half-lives the mass will be
`(m_0)/(4)`, and so on..
Therefore, after x half-lives the mass of the sample will be

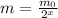
`m= (m_0)/(2^x)` (1)
In our problem, the initial mass is
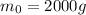
`m_0 = 2000 g` while the mass after x half-lives is
`m=125 g`, so by using equation (1) we can find the value of x:

`2^x = (m_0)/(m)= (2000 g)/(125 g)=16`
From which

`x=4`
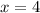
And the correct answer is C).