Question

Assume the hold time of callers to a cable company is normally distributed with a mean of 3.53.5 minutes and a standard deviation of 0.20.2 minute. Determine the percent of callers who are on hold between 3.43.4 minutesminutes and 3.83.8 minutes.

Answer 1

62.47%

Explanation:

Mean =
`\mu = 3.5`

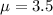
Standard deviation =
`\sigma = 0.2`

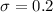
We are supposed to find the percent of callers who are on hold between 3.4 minutes and 3.8 minutes.

Formula :
`z=(x-\mu)/(\sigma)`

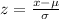
At x = 3.4

`z=(3.4-3.5)/(0.2)`

`z=-0.5`

At x =3.8

`z=(3.8-3.5)/(0.2)`

`z=1.5`

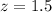
We are supposed to find P(3.4<z<3.8)

Using z table

So, P(3.4<z<3.8)=P(-0.5<z<1.5)=P(z<1.5)-P(z<-0.5) = 9332-0.3085=0.6247= 62.47%

So, the percent of callers who are on hold between 3.4 minutes and 3.8 minutes is 62.47%

Answer 2

We calculate z-scores associated with x = 3.4 and x = 3.8.
For x = 3.4, z = (3.4 - 3.5) / (0.2) = -0.5
For x = 3.8, z = (3.8 - 3.5) / (0.2) = 1.5
Then we calculate the probability that -0.5 < z < 1.5 from z-tables.
P(-0.5 < z < 1.5) = 0.6247 = 62.47% of callers on hold between 3.4-3.8 minutes.