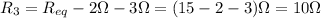Question

The current in the circuit shown is 2.0 A.

What is the value of R3?

10 Ω
15 Ω
20 Ω
55 Ω

answer was a

Answer 1

10 Ω

Step-by-step explanation:

I got it right

Answer 2

Ohm's law allows us to find the equivalent resistance of the circuit. In fact:

`V=IR_(eq)`
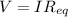
where
V is the voltage of the battery
I is the current in the circuit

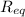
`R_(eq)` is the equivalent resistance

Re-arranging the equation and using the data of the problem, we get

`R_(eq)= (V)/(I)= (30 V)/(2.0 A) =15 \Omega`

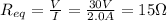
The three resistors are in series, so their equivalent resistance is just the sum of the three resistances:

`R_(eq)= 2 \Omega + 3 \Omega + R_3`
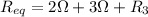
Since we know the value of the equivalent resistance,
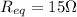
`R_(eq)=15 \Omega`, we can find the value of R3:

`R_3 = R_(eq) - 2 \Omega - 3 \Omega = (15-2-3) \Omega = 10 \Omega`