Question

GEOMETRY

*image is attached above*

Answer 1

(-9.5, -4)

Explanation:

Given the ratio a:b (a to b) of two segments formed by a point of partition, and the endpoints of the original segment, we can calculate the point of partition using this formula:

`( (a )/(a + b) (x_(2) - x_(1)) + x_(1), (a)/(a + b) (y_(2) - y_(1))+y_(1))`.

Given two endpoints of the original segment

→ (-10, -8) [(x₁, y₁)] and (-8, 8) [(x₂, y₂)]

Along with the ratio of the two partitioned segments

→ 1 to 3 = 1:3 [a:b]

Formed by the point that partitions the original segment to create the two partitioned ones

→ (x?, y?)

We can apply this formula and understand how it was derived to figure out where the point of partition is.

Here is the substitution:

x₁ = -10

y₁ = -8

x₂ = -8

y₂ = 8

a = 1

b = 3

`( (a )/(a + b) (x_(2) - x_(1)) + x_(1), (a)/(a + b) (y_(2) - y_(1))+y_(1))`. →

`( ((1) )/((1) + (3)) ((-8) - (-10)) + (-10), ((1))/((1) + (3)) ((8) - (-8))+ (-8))` →

`( (1)/(4) ((-8) - (-10)) + (-10), (1)/(4)((8) - (-8)) + (-8))` →

`( (1)/(4) (2) + (-10), (1)/(4)(16) + (-8))` →

`( ((1)/(2)) + (-10), (4) + (-8))` →

`( (-(19)/(2)), (-4))` →

`( -(19)/(2), -4)` →

*
`( -9.5, -4)`*

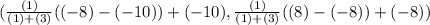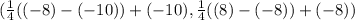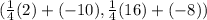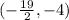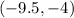Now the reason why this