Answer:
The dimensions of the sides of the fruit stand are 3.5 feet , 2.0 feet and 3.2 feet. Option B is correct.
Explanation:
Given information:
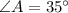 ,
,
 and
and
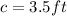 .
.
According to the angle sum property of a triangle, the sum of all interior angles of a triangle is 180 degree.
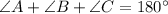
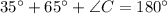
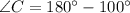
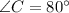
According to Law of sines

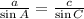
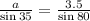
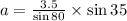
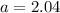
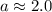
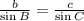
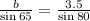
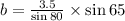
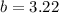
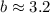
Therefore the dimensions of the sides of the fruit stand are 3.5 feet , 2.0 feet and 3.2 feet. Option B is correct.