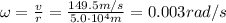Question

The Tornado has a radius of 4.0m and takes 2.0 s to make a revolution. What is Jermy's angular velocity?

A plane is circling the airport. It takes 35 min ( convert to seconds) to do one circle with a radius of 5.0 x 10^4 m. The plane weighs 6.05 x 10^4 kg. What the angular velocity?

Answer 1

part a)
The angular velocity is the ratio between the tangential velocity and the radius of the orbit:

`\omega = (v)/(r)`
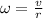
we already have the radius of the orbit, r=4.0 m, but we have to find the tangential velocity v.
We know that the perimeter of the orbit is

`d=2 \pi r = 2 \pi (4.0 m)=25.12 m`
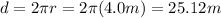
And that the Tornado takes t=2.0 s to make one revolution (so, it takes 2.0s to complete one perimeter), so the tangential velocity is

`v= (d)/(t)= (25.12 m)/(2.0 s)=12.56 m/s`

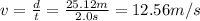
Therefore, the angular velocity is

`\omega= (v)/(r)= (12.56 m/s)/(4.0 m)=3.14 rad/s`

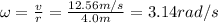
part b) The time the plane takes to do one circle is

`t=35 min = 2100 s`
Similarly to what we have done before, the perimeter of the orbit is

`d=2 \pi r= 2 \pi (5.0 \cdot 10^4 m)=3.14 \cdot 10^5 m`
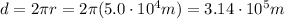
And so the tangential velocity is

`v= (d)/(t)= (3.14 \cdot 10^5 m)/(2100 s)=149.5 m/s`

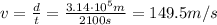
And the angular velocity of the plane is given by

`\omega = (v)/(r)= (149.5 m/s)/(5.0 \cdot 10^4 m)=0.003 rad/s`