Question

The cost of renting tuxes for the Choral Society's formal is $24 down, plus $89 per tux. Express the cost C as a function of x, the number of tuxedos rented.

Use your function to answer the following questions.(a) What is the cost of renting two tuxes? 
$  

(b) What is the cost of the second tux? 
$  

(c) What is the cost of the 4,098th tux? 
$  

(d) What is the variable cost? $ 


What is the fixed cost? 
$  

What is the marginal cost? 
$

Answer 1

a) The formula would be C = 89x + 24.

b) To find the cost of 2 tuxes, just plug in 2 for x and you get 202.

c) For the 4098th tux, plug in 4098 for x and you get $364,746.

d) The variable cost is the number of tuxes.
The fixed cost is the $24 down. The marginal cost is $89, the amount that it changes for each tux.

Answer 2

Let
`x` be the number of tuxedos and
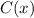
`C(x)` the cost of the number of tuxedos rented.
We know for our problem that the cost of renting a tuxedo is $89, so the cost of renting
`x` tuxedos will be
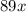
`89x`. We also know that the down payment is $24, so it is a single payment of 24$ no matter how many tuxedos are rented. Knowing all of this, we can conclude that the total cost of renting
`x` will be represented by the function:

`C(x)=89x+24`

(a) To find the cost of renting two tuxedos, we are going to evaluate our function at
`x=2`. In other words, we are going to replace
`x` with 2 in our function:

`C(x)=89x+24`

`C(2)=89(2)+24`

`C(2)=178+24`

`C(2)=202`

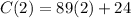
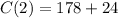
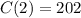
We can conclude that the cost of renting two tuxedos is $202

(b) To find the cost of the second tux, we need to find the average cost function first. To do that we are going to divide our cost function
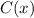
`C(x)` by
`x`:

`avC(x)= (C(x))/(x)`

`avC(x)= (89x+24)/(x)`

`avC(x)= (89x)/(x) + (24)/(x)`

`avC(x)=89+ (24)/(x)`

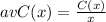
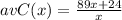
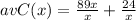
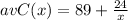
Now that we have our average cost function, we are going to evaluate it at
`x=2`:

`avC(x)=89+ (24)/(x)`

`avC(2)=89+ (24)/(2)`

`avC(2)=89+12`

`avC(2)=101`

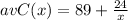
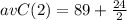
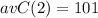
We can conclude that the cost of the second tux is $101

(c) Just like before, to find the cost of the 4,098th tux, we are going to evaluate our average cost function at
`x=4098`. In other words we are going to replace
`x` with 4098 in our average cost function from our previous point:

`avC(x)=89+ (24)/(x)`

`avC(4098)=89+ (24)/(4098)`

`avC(x)=89.001`

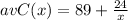
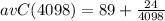
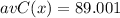
We can conclude that the cost of the 4,098th tux is $89.001

(d) Variable costs are the costs that vary in direct proportion to the quantity of items. In our case the quantity of tuxedos. Looking at our function the only thing that is changing is the number of tuxedos, so the variable cost of our function is
`85x`.
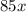Fixed cost on the other hand are costs that are independent of the number of items. In our case the down payment. Does not matter how many tuxedos we rent, the down payment will always be $24. So, in our function the fixed cost is 24.

We can conclude that the variable cost is
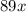`89x` and the fixed cost is
`24`.

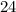(e) The marginal cost is the change in total cost that when the number of items rented increases by one unit. To find our marginal cost, we are going to fin
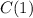`C(1)` and
`C(2)` in our cost function, and then, we are going to subtract the outputs:

`C(x)=89x+24`

`C(1)=89(1)+24`

`C(1)=89+24`

`C(1)=113`


`C(2)=89(2)+24`

`C(2)=178+24`

`C(2)=202`

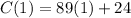
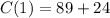
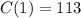
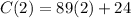
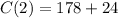
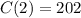
Now, we can subtract the output of
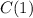`C(1)` from the output of
`C(2)`:

`202-113=89`

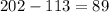
We can conclude that the marginal cost is $89