Answer:
Option (a) is correct.
The recursive rule for the given sequence
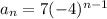 is
is
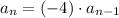 with
with

Explanation:
The explicit sequence of the geometric sequence is given by:

where,
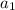 is the first term
is the first term
r is the common ratio
n is the number of terms
For the given explicit rule,
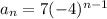
Comparing with above sequence , we have,
 and r = -4
and r = -4
Recursive formula for the geometric sequence having
 and r = -4 is given by:
and r = -4 is given by:
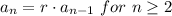
Putting values, we get,
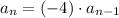
Hence, the recursive rule for the given sequence
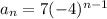 is
is
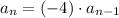 with
with

hence, option (a) is correct.