Question

A 535 kg roller coaster car began at rest at the top of a 93.0 m hill. Now it is at the top of the first loop-de-loop.

This roller coaster’s track is nearly frictionless, so resistance can be ignored. Using g = 9.8 m/s2, what best describes the roller coaster car when it is at the top of the loop-de-loop?

A) The car has only potential energy, so it is moving at 0 m/s.
B) The car has both potential and kinetic energy, and it is moving at 24.6 m/s.
C) The car has both potential and kinetic energy, and it is moving at 34.9 m/s.
D) The car’s potential energy has all been converted to kinetic energy, so it moves at 42.7 m/s.

Answer 1

B) The car has both potential and kinetic energy, and it is moving at 24.6 m/s.

Step-by-step explanation:

Since the track is frictionless, the total mechanical energy of the car is constant, and it is always sum of the kinetic energy (K) and potential energy (U):

`E=K+U`

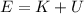
At the beginning, when the car is at rest at the top of the hill, all its energy is just gravitational potential energy (because the velocity is zero, so the kinetic energy is zero), so the mechanical energy is:

`E=U_0=mgh=(535 kg)(9.8 m/s^2)(93.0 m)=487,599 J`

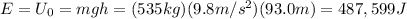
At the top of the loop-de-loop, the car will have both potential energy (because it has a certain height above the ground) and kinetic energy (because it has some speed), but the total will still be the same:

`E=U+K=487,599 J`

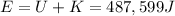
We can calculate the potential energy at this point:

`U=mgh=(535 kg)(9.8 m/s^2)(62.0 m)=325,066 J`

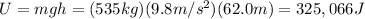
So, the kinetic energy must be

`K=E-U=487,599 J-325,066 J=162,533 J`

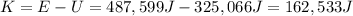
And since the kinetic energy is related to the speed v by:

`K=(1)/(2)mv^2`

we can find the speed of the car at the top of the loop-de-loop:

`v=\sqrt{(2K)/(m)}=\sqrt{(2\cdot 162,533 J)/(535 kg)}=24.6 m/s`

Answer 2

Using g = 9.8 m/s2, the statement that best describes the roller coaster car when it is at the top of the loop-de-loop is that The car has both potential and kinetic energy, and it is moving at 24.6 m/s. The correct answer is B) The car has both potential and kinetic energy, and it is moving at 24.6 m/s.