Question

If x equals 6, what is the order of the angles from smallest to largest degree?

Answer 1

∠B < ∠A < ∠C

Explanation:

Given,

In triangle ABC,

`AB=x^2+(x)/(2)`

`BC=x^2+(x)/(3)`

`CA=x^2-(x)/(2)`

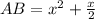
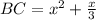
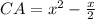
At x = 6,

`AB=6^2+(6)/(2)=36 + 3 = 39`

`BC=6^2+(6)/(3)=36 + 2 = 38`

`CA=6^2-(6)/(2)=36 - 3 = 33`

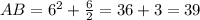
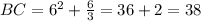
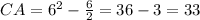
We know that in a triangle, the interior angle opposite to largest side is largest, opposite to smallest side is smallest and opposite to medium side is medium.

Here, CA < BC < AB

Also, angles A, B and C are opposite angles of the sides BC, CA and AB respectively,

Hence, ∠B < ∠A < ∠C

Which is the required order of angles.

Answer 2

The size of the angle is always corresponding to the opposite side to it, for example
∠A corresponds to side BC
∠C corresponds to side AB
∠B corresponds to side AC
thus given x=6 then:
AC=x^2-x/2=33
AB=x^2+x/2=39
BC=x^2+x/3=34
thus the order of angles from the smallest to the largest is ∠B, ∠A, ∠C