Answer:
The correct option is D. The average rate of change between n = 1 and n = 3 is 4.
Explanation:
The given sequence is defined as
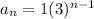
The average rate of change from x₁ and x₂ is

At x=1,
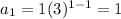
At x=3,
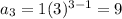
The average rate of change between n = 1 and n = 3.

The average rate of change between n = 1 and n = 3 is 4. Therefore option D is correct.