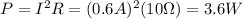Question

A 9 Volt battery is hooked up to two resistors in series. One has a resistance of 5 Ohms, and the other has a resistance of 10 Ohms. Through which resistor is energy being dissipated at the higher rate?

Answer 1

The power dissipated through a resistor is given by

`P=I^2 R`
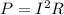
where I is the current and R the resistance.

The two resistors are connected in series, so they are crossed by the same current I. This means that the power dissipated on the two resistors depends only on the value of the resistance, according to
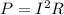
`P=I^2 R`, and so the resistor of
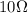
`10 \Omega` will dissipate more energy than the resistor of
`5 \Omega`.

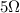
We can also solve the problem numerically. The equivalent resistance of the circuit is given by:

`R_(eq)= 5 \Omega + 10 \Omega= 15 \Omega`
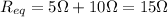
So the current flowing in the circuit is

`I= (V)/(R_(eq)) = (9 V)/(15 \Omega)=0.6 A`

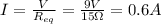
Therefore, the power dissipated on the resistor of
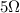
`5 \Omega` is

`P=I^2 R = (0.6 A)^2 (5 \Omega)=1.8 W`
while the power dissipated on the resistor of
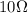
`10 \Omega` is

`P=I^2 R=(0.6 A)^2 (10 \Omega)=3.6 W`