Question

Landon is standing in a hole that is 5.1 ft deep. He throws a rock, and it goes up into the air, out of the hole, and then lands on the ground above. The path of the rock can be modeled by the equation y = -0.005x2 + 0.41x - 5.1, where x is the horizontal distance of the rock, in feet, from Landon and y is the height, in feet, of the rock above the ground. How far horizontally from Landon will the rock land?

Answer 1

When the rock hits the ground, y = 0

-.005x^2 +0.41x -5.1 = 0

Multiply equation by (-200)

x^2 -82x +1020 = 0

Use quadratic formula:

`x = (-b \pm √(b^2 - 4ac))/(2a) = (82 \pm √(82^2 -4(1)(1020)))/(2) \\ \\ x = (82 \pm 51.4198)/(2) \\ \\ x = 15.29 , 66.71`

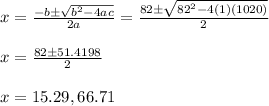
Since the ball is initially below the ground, on its way up it will reach the point where y=0 but still be in the air, therefore the ball lands the second time y=0 or when x is larger.

Answer: 66.71 feet

Answer 2

A graphing calculator shows the rock will land 66.71 ft horizontally from where Landon is standing.

_____
You can also figure the distance using the quadratic formula to solve
-0.005x² +0.41x -5.1 = 0
x = (-0.41 -√(0.41² -4(-.005)(-5.1)))/(2*(-.005))
= (-0.41 -√0.0661)/-0.01
= 66.7099 . . . . feet