Question

Which of the following tables shows the correct steps to transform x2 + 6x + 8 = 0 into the form (x − p)2 = q? [p and q are integers]

A. Step 1 x2 + 6x + 8 − 1 = 0 − 1
Step 2 x2 + 6x + 7 = −1
Step 3 (x + 3)2 = −1

B. Step 1 x2 + 6x + 8 + 1 = 0 + 1
Step 2 x2 + 6x + 9 = 1
Step 3 (x + 3)2 = 1

C. Step 1 x2 + 6x + 8 − 2 = 0 − 2
Step 2 x2 + 6x + 6 = −2
Step 3 (x + 3)2 = −2

D. Step 1 x2 + 6x + 8 + 2 = 0 + 2
Step 2 x2 + 6x + 10 = 2
Step 3 (x + 3)2 = 2

Answer 1

B would be the correct answer, i also just took the test and got it correct!

Answer 2

To express a quadratic function of the form
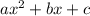
`a x^(2) +bx+c` into its vertex form
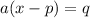
`a(x-p)=q` (p and q are integers), we are going to use the completing square method:
Step 1
Add 1 to both sides of the equation:

`x^2+6x+8=0`

`x^2+6x+8+1=0+1`
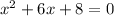
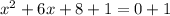
Step 2
Perform the operations:

`x^2+6x+9=1`
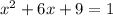
Step 3
Notice that
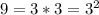
`9=3*3=3^2`, so we can rewrite our expression as follows:

`x^2+6x+3^2=1`

`(x+3)^2=1`

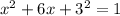
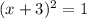
We can conclude that the correct steps to transform x2 + 6x + 8 = 0 into the form (x − p)2 = q [p and q are integers] are:
B. Step 1 x2 + 6x + 8 + 1 = 0 + 1
Step 2 x2 + 6x + 9 = 1
Step 3 (x + 3)2 = 1