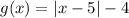Question

If you apply the changes below to the absolute value parent function, f(x) = |x|, which of these is the equation of the new function? Shift 5 units to the right. Shift 4 units down.

Answer 1

The equation of the transformed function is:

`g(x)=|x-5|-4`

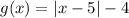
Explanation:

We are given a absolute value parent function f(x) by:

`f(x)=|x|`

Now we have to apply some transformation to this parent function in order to get the transformed function.

The transformations that are applied are:

Shift 5 units to the right. Shift 4 units down.

We know that:

The shift of the parent function a units to the left or right is given by:

`g(x)=f(x+a)`

If a>0 then the shift is a units to the left

and if a<0 then the shift is a units to the right.

Also, the shift of k units to the left and right of some parent function f(x) is given by:

`g(x)=f(x)+k`

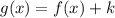
if k<0 then the shift is downward.

and if k>0 then the shift is upward.

So, here the equation of the transformed function is:

`g(x)=|x-5|-4`

Answer 2

For a right shift of 5, you replace x with x-5.
For a down shift of 4, you replace f(x) with f(x)-4.

The new function is ...
|x -5| -4