Answer:
The given sequences are
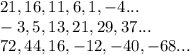
The first sequence is decreasing by a difference of 5, that is
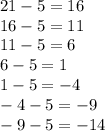
So, the next two terms are -9 and -14.
The second sequence is increasing by a difference of 8, that is
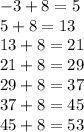
So, the next two terms are 45 and 53
The third and last sequence is decreasing by a difference of 28, that is
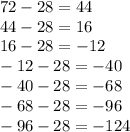
So, the next two terms of this sequence are -96 and -124.