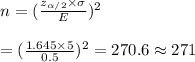Question

The advertising department of a nationally circulated magazine wishes to estimate the mean age of.its subscribers to within 0.5 year with 90% confidence. if they estimate that the standard deviation of the ages of their subscribers is 5 years, find the required sample size.

a. 165
b. 17
c. 271
d. 45 1 points first question previous question question 14 of 30 next question last question

Answer 1

The correct answer is C) 271.

We first find the z-score associated with this confidence interval:
Convert 90% to a decimal: 90/100 = 0.9
Subtract from 1: 1 - 0.9 = 0.1
Divide by 2: 0.1/2 = 0.05
Subtract from 1: 1 - 0.05 = 0.95

Looking this value up in a z-table, we see that this number is the same distance from 1.64 and 1.65; therefore we will use 1.645.

Now we will use the following formula to calculate the sample size required:

`n=((z_(\alpha/2)*\sigma)/(E))^2 \\ \\=((1.645*5)/(0.5))^2=270.6\approx 271`