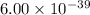Answer : The value of
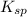 is
is
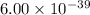
Explanation :
The solubility equilibrium reaction will be:
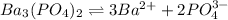
Let the molar solubility be 's'.
The expression for solubility constant for this reaction will be,
![K_(sp)=[Ba^(2+)]^3[PO_4^(3-)]^2](https://img.qammunity.org/2019/formulas/chemistry/college/nguh7e1uopdf10n0a7awal6qknl1p1iopx.png)
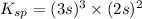
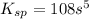
Given:
Molar solubility of
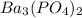 = s =
= s =
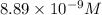
Now put all the given values in the above expression, we get:
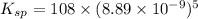
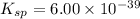
Therefore, the value of
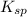 is
is