Question

Find the indicated limit, if it exists. limit of f of x as x approaches 9 where f of x equals x plus 9 when x is less than 9 and f of x equals 27 minus x when x is greater than or equal to 9

The limit does not exist.
18
0
9

Answer 1

18

Explanation:

Answer 2

B. 18

Explanation:

For the function

`f(x)=\left\{\begin{array}{l}x+9,\ \ x<9\\27-x,\ \ x\ge 9\end{array}\right.`

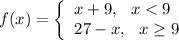
we can find the value of the function for all x that are very close to 9 but are less than 9 and for all values of x that are very close to 9 but are greater than 9.

1. For
`x<9:`

`\lim \limits_(x\rightarrow 9)f(x)=\lim \limits_(x\rightarrow 9)(x+9)=9+9=18`

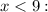
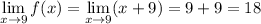
2. For
`x\ge 9:`

`\lim \limits_(x\rightarrow 9)f(x)=\lim \limits_(x\rightarrow 9)(27-x)=27-9=18`

So, limit exists and is equal to 18.