Question

What is the y value of the vertex of 4x^2+8x-8

Answer 1

The y-value of the vertex is
`-12`

Explanation:

we know that

The equation of a vertical parabola into vertex form is equal to

`f(x)=a(x-h)^(2)+k`

where

(h,k) is the vertex of the parabola

In this problem we have

`f(x)=4x^(2)+8x-8` -----> this a vertical parabola open upward

Convert to vertex form

Group terms that contain the same variable, and move the constant to the opposite side of the equation

`f(x)+8=4x^(2)+8x`

Factor the leading coefficient

`f(x)+8=4(x^(2)+2x)`

Complete the square. Remember to balance the equation by adding the same constants to each side

`f(x)+8+4=4(x^(2)+2x+1)`

`f(x)+12=4(x^(2)+2x+1)`

Rewrite as perfect squares

`f(x)+12=4(x+1)^(2)`

`f(x)=4(x+1)^(2)-12`

The vertex is the point
`(-1,-12)`

The y-value of the vertex is
`-12`

Answer 2

To find the vertex,
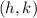
`(h,k)`, or a quadratic of the form
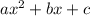
`ax^2+bx+c`, we are going to use the vertex formula:
`h= (-b)/(2a)`, and then, we are going to evaluate the function at
`h` to find
`k`:

We can infer four our quadratic 4x^2+8x-8 that
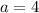
`a=4` and
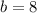
`b=8`, so lets replace those values in our formula to find
`h`:

`h= (-b)/(2a)`

`h= (-8)/((2)(4))`

`h= (-8)/(8)`

`h=-1`

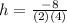
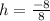
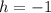
To find
`k` we are going to evaluate the quadratic at
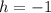
`h=-1`. In other words, we are going to replace
`x` with -1:

`4x^2+8x-8`

`k=4(-1)^2+8(-1)-8`

`k=4-8-8`

`k=-12`

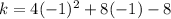
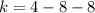
Our vertex is (-1,-12). We can conclude that the y value of the vertex of 4x^2+8x-8 is -12.