Question

For the polynomial below, -1 is a zero. g(x) = x2-3x² + 25x +29 Express g (x) as a product of linear factors.

Answer 1

Hello there. To solve this question, we'll have to remember some properties about polynomials.

We want to express the following 3rd degree polynomial as a product of linear factors:

`g(x)=x^3-3x^2+25x+29`

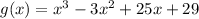
Knowing that -1 is a zero.

For this, there are two ways of determining the other roots and hence the linear factors.

Remember that a polynomial is written as a product of linear factors if

`f(x)=a(x-x_1)(x-x_2)\cdots`

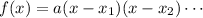
Where x1, x2 ... are the roots of the polynomial.

It is also called the canonical form of the polynomial.

First way: divide g(x) by (x - (-1)), that is (x + 1)

We'll use the long division method for polynomials:

At the top of x + 1 in the diagram below, we add the terms that, when multiplied by the bottom expression, gives us a term that can be subtracted from g(x).

We have a x³ factor, so we want to multiply it first by x² in order to cancel out:

Now we have a -4x² factor, so we multiply it by -4x in order to cancel out:

Finally, multiply it by a 29 in order to cancel the first 29x term:

Hence we say that

`x^3-3x^2+25x+29=(x+1)(x^2-4x+29)`

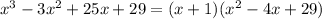
Now, we want to factorize the quadratic expression in the right hand side, writing it as a product of linear factors as well:

As said before, we can take the roots of the expression and write it in canonical form. Since it is a quadratic expression, we have this easier formula to find the roots:

`ax^2+bx+c=0\Rightarrow x=(-b\pm√(b^2-4ac))/(2a)`

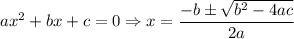
Plugging a = 1, b = -4 and c = 29, we'll get

`\begin{gathered} x=(-(-4)\pm√((-4)^2-4\cdot1\cdot29))/(2\cdot1) \\ \\ x=(4\pm√(16-116))/(2)=(4\pm√(-100))/(2) \\ \end{gathered}`

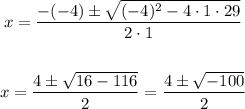
Notice the radical is a negative number, hence it cannot be factored in terms of real linear factors.

We say that for an expression

`x^2+\beta x+\gamma`

It is not reducible over R (real numbers) if

`\beta^2-4\gamma<0`

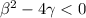
Therefore the final answer is:

`(x+1)(x^2-4x+29)`

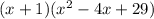
We could also use the following method to find this answer:

It is called the Horner-Ruffini method, that we dispose the coefficients and the roots in the following manner

Multiply the first coefficient by the root and add it to the second number in the line. Repeat the process until you reach the last number.

Therefore the result of this division is the polynomial:

`x^2-4x+29`

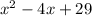
As we found before.