Answer:
Emily will earn $166 more interest than Katie after the interest period ends for each account.
Explanation:
Formula for compound interest is:
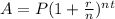 , where P is the initial amount, A is the final amount with interest, r is the rate of interest in decimal, n is the number of compounding in a year and t is the time duration
, where P is the initial amount, A is the final amount with interest, r is the rate of interest in decimal, n is the number of compounding in a year and t is the time duration
Katie invests $5,000 in an account earning 4% interest, compounded annually for 5 years. That means here,
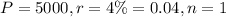 and
and

So,
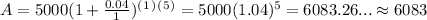
Thus, the amount of interest earned by Katie
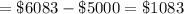
Now, Emily invests $10,000 in an account earning 4% interest, compounded annually for 3 years. That means here,
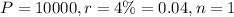 and
and
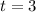
So,
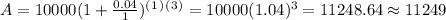
Thus, the amount of interest earned by Emily
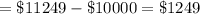
After the interest period ends for each account, Emily will earn ($1249 - $1083) or $166 more interest than Katie.