Question

Please help!!
Everything is in the photo

Answer 1

a) Pine Road and Oak Street form a right angle, so we can extract the relation


`\tan30^\circ=\frac x{11\sqrt3}\implies\frac1{\sqrt3}=\frac x{11\sqrt3}\implies x=11`

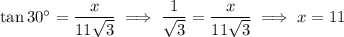
where
`x` is the distance we want to find (bottom side of the rectangle).

Alternatively, we can use the other given angle by solving for
`x` in


`\tan60^\circ=\frac{11\sqrt3}x`

but we'll find the same solution either way.

b) Pine Road and Oak Street form a right triangle, with Main Street as its hypotenuse. We can use the Pythagorean theorem to find how long it is.


`(\text{Pine})^2+(\text{Oak})^2=(\text{Main})^2`

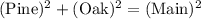
Let
`y` be the length of Main Street. Then


`(11\sqrt3)^2+11^2=x^2\implies x^2=484\implies x=\pm22`

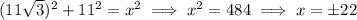
but of course the distance has to be positive, so
`x=22`.