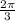Question

Determine whether the function is periodic. If it is periodic, find the period. f(x) = 3 sin 2x + 4 cos 3x

Answer 1

All sums of trigonometric functions are periodic.

This function has a period of 2π by observation.

Answer 2

`(2\pi)/(3)`

Explanation:

We are given that a function

`f(x)=3 sin 2x +4 cos 3x`

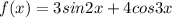
We have to find that given function is periodic or not and if given function is periodic then find the period

We know that if a function is periodic then

`f(x+c)=f(x)`

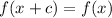
We know that sin x and cos x are periodic function with period
`2\pi`

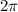
Sum of periodic function is also periodic

Hence, given function is periodic function.

Period of sin x=
`2\pi`

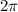
Then,
`2 x=2\pi`

`x=\pi`

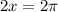
Period of cos x is
`2\pi`

`3x=2\pi`

`x=(2\pi)/(3)`

`( lcm(\pi,2\pi)/(lcm (1,3))=(2\pi)/(3)`

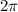
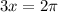
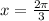
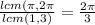
Hence, period of given function is
`(2\pi)/(3)`