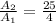Circle Q and circle R have a central angle measuring 75°. The ratio of circle Q's radius to circle R's radius is 2:5. Which ratio represents the area of the sector for…

Question

asked May 26, 2019 160k views

1 Answer

Gnas · Answer 1 · 2019-06-02T12:01:37+0000

In this question, it is given that

Circle Q and circle R have a central angle measuring 75°. The ratio of circle Q's radius to circle R's radius is 2:5.

And the formula of area of sector is

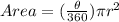
$Area = ( ( \theta)/(360 )) \pi r^2$

And the radius are in the ratio 2:5.

Let the radius are 2x and 5x. SO area of sectors are

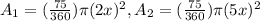
$A_(1) = ( (75)/(360) ) \pi (2x)^2, A_(2)= ( (75)/(360) ) \pi (5x)^2$

And the ratio is

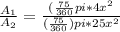
$(A_(1) )/(A_(2)) = \frac { ( (75)/(360) pi *4x^2}{ ( (75)/(360)) pi*25x^2}$

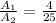
(A_(1))/(A_(2)) = (4)/(25)

So for the ratio of the area of sectors of circle R to Q, it is

(A_(2))/(A_(1)) = (25)/(4)