Question

ABC is formed by two tangents intersecting outside of a circle. If minor arc AC = 98°, what is the measure of ∠ABC?

Answer 1

It's 82 degrees. Subtract your minor arc (98) by 360 to get your major arc, which is 262. Then, subtract 98 (minor arc) from 262 (major arc), which gives you 164. Finally, divide 164 by 2 to get angle ABC.

Answer 2

`m\angle ABC=82^(o)`

Step-by-step explanation:

Since tangent-tangent angle theorem states that the measure of angle formed by two tangents intersecting outside of a circle is one half the difference of the intercepted arcs (manor arc-minor arc)

First of all we will find the measure of major arc by subtracting 98 from 360 as a circle is 360 degrees all the way around.

`\text{Major arc}=360-\text{Minor arc}`

`\text{Major arc}=360-98=262`

`m\angle ABC=\frac{\text{Major arc-Minor arc}}{2}`

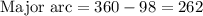
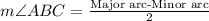
Upon substituting our values in above formula we will get,

`m\angle ABC=(262-98)/(2)`

`m\angle ABC=(164)/(2)`

`m\angle ABC=82`

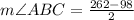
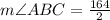
Therefore, the measure of angle ABC is 82 degrees.