Answer:
The speed needed to escape from the solar system starting from the surface of Neptune is approximately 23557.615 meters per second.
Step-by-step explanation:
The escape speed needed to escape from the gravitational influence of a planet (
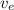 ), measured in meters per second, is derived from Newton's Law of Gravitation and Principle of Energy Conservation and defined by the following formula:
), measured in meters per second, is derived from Newton's Law of Gravitation and Principle of Energy Conservation and defined by the following formula:
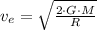 (1)
(1)
Where:
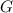 - Gravitational constant, measured in cubic meters per kilogram-square second.
- Gravitational constant, measured in cubic meters per kilogram-square second.
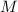 - Mass of Neptune, measured in kilograms.
- Mass of Neptune, measured in kilograms.
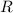 - Radius from the center to surface, measured in kilograms.
- Radius from the center to surface, measured in kilograms.
If we know that
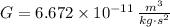 ,
,
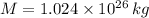 and
and
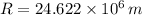 , then the escape speed needed is:
, then the escape speed needed is:
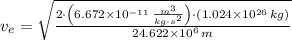
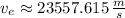
The speed needed to escape from the solar system starting from the surface of Neptune is approximately 23557.615 meters per second.