Question

What is the equation for the translation of x^2 + y^2 = 81 six units to the left and five units up?

Answer 1

The formula would be (x + 6)^2 + (y - 5)^2 = 81.

This is the equation for a circle. We added plus 6 to the x term to get it to move to the left. And we add minus 5 to the y term to get it to move up 5 units.

Answer 2

The equation for the translation of the given circle is:

`(x+6)^2+(y-5)^2=81`

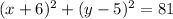
Explanation:

The original equation is given by:

`x^2+y^2=81`

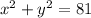
This means that the equation represents a circle whose center is at origin (0,0) and radius 9.

( Since the standard form of a circle with center at (h,k) and radius r is given by:

`(x-h)^2+(y-k)^2=r^2` )

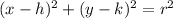Now, when the circle is shifted six units to the left and five units up then the change in each of the coordinates is given by:

(x,y) → (x-6,y+5)

i.e. the center of the circle (0,0) will be changed to

(0,0) → (0-6,0+5) =(-6,5)

Also, there is no change in the size of the figure on translation.

Hence, the radius of the circle remains same.

Hence, the transformed equation is given by:

`(x-(-6))^2+(y-5)^2=81\\\\i.e.\\\\(x+6)^2+(y-5)^2=81`