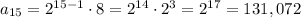Question

How would I write this as a geometric recursive and explicit formula? Algebra 2

Answer 1

Denote the sequence by
`a_n` with
`n\ge1`.

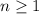
Recursively:

The first number is
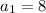
`a_1=8`, and each successive number is twice the previous one. So
`a_2=16`,
`a_3=32`,
`a_4=64`, ... .

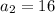
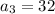
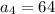
In other words,


`a_2=2a_1`

`a_3=2a_2`

`a_4=2a_3`

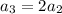
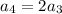
and so in general,


`a_n=2a_(n-1)`

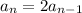
Explicitly:

We can arrive at this formula by, in a way, working backwards. If
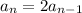
`a_n=2a_(n-1)`, that means
`a_(n-1)=2a_(n-2)`, and so
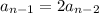
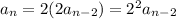
`a_n=2(2a_(n-2))=2^2a_(n-2)`, and so on. We would end up with


`a_n=2a_(n-1)=2^2a_(n-2)=2^3a_(n-3)=\cdots=2^(n-2)a_2=2^(n-1)a_1`

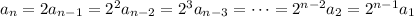
(You'll notice a pattern here: the exponent of the 2 and the index of the earlier term in the sequence add up to
`n`. For example,
`2^1a_(n-1)\implies 1+(n-1)=n`.)

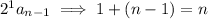
or simply


`a_n=2^(n-1)\cdot8`

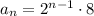
Then the 15th term is obtained immediately by evaluating this rule at
`n=15`. We get


`a_(15)=2^(15-1)\cdot8=2^(14)\cdot2^3=2^(17)=131,072`