Question

Determine the gravitational field 300km above the surface of the earth. How does this compare to the field on the earth's surface?

Answer 1

The strength of the gravitational field is given by:

`g= (GM)/(r^2)`
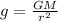
where
G is the gravitational constant
M is the Earth's mass
r is the distance measured from the centre of the planet.

In our problem, we are located at 300 km above the surface. Since the Earth radius is R=6370 km, the distance from the Earth's center is:

`r=R+h=6370 km+300 km=6670 km= 6.67 \cdot 10^(6) m`

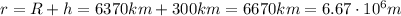
And now we can use the previous equation to calculate the field strength at that altitude:

`g= (GM)/(r^2)= ((6.67 \cdot 10^(-11) m^3 kg^(-1) s^(-2))(5.97 \cdot 10^(24) kg))/((6.67 \cdot 10^6 m)^2) = 8.95 m/s^2`

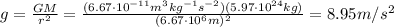
And we can see this value is a bit less than the gravitational strength at the surface, which is
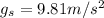
`g_s = 9.81 m/s^2`.