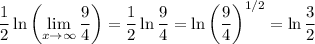Question

Only the letter g) and I know it’s infinity - infinity but I don’t know how to modify it to be able to find the answer

Answer 1

You have to use some properties of logarithms. I'm assuming the logarithm is real-valued, in which case the following hold:


`\ln a-\ln b=\ln\frac ab`

`\ln a^n=n\ln a`

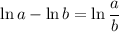
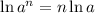
for real
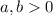
`a,b>0` and all real
`n`.

So we can write


`\ln√(9x+2)-\ln√(4x+5)=\ln(9x+2)^(1/2)-\ln(4x+5)^(1/2)`

`=\ln((9x+2)^(1/2))/((4x+5)^(1/2))`

`=\ln\left((9x+2)/(4x+5)\right)^(1/2)`

`=\frac12\ln(9x+2)/(4x+5)`

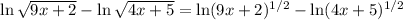
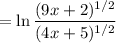
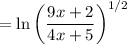
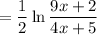
In taking the limit, we're considering
`x` as it gets arbitrarily large. We know that for
`x>0`,
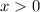
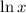
`\ln x` is continuous. This means we can pass the limit through the logarithm:


`\displaystyle\lim_(x\to\infty)\frac12\ln(9x+2)/(4x+5)=\frac12\ln\left(\lim_(x\to\infty)(9x+2)/(4x+5)\right)`

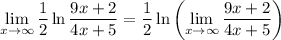
so now we're only concerned with the limit of a rational function. The leading terms in the numerator and denominator both have the same power, so we only need to consider their coefficients. In other words,


`(9x+2)/(4x+5)\approx(9x)/(4x)=\frac94`

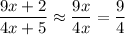
when
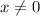
`x\\eq0`, and so the limit is the same as


`\displaystyle\frac12\ln\left(\lim_(x\to\infty)\frac94\right)=\frac12\ln\frac94=\ln\left(\frac94\right)^(1/2)=\ln\frac32`