By definition, the of a line written in Standard form is:
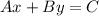
Where "A", "B" and "C" are Integers ("A" is positive).
The Slope-Intercept form of the equation of a line is:

Where "m" is the slope and "b" is the y-intercept.
You know that this line passes through these points:

By definition, the value of "x" is zero when the line intersects the y-axis. Then, you can identify that, in this case:
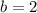
Now you can substitute the value of "b" and the coordinates of the second point into the following equation and solve for "m":

Then, the slope of the line is:

Therefore, the equation of this line in Slope-Intercept form is:
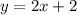
To write it in Standard form, you can follow these steps:
- Subtract 2 from both sides of the equation:
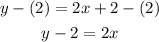
- Subtract "y" from both sides of the equation:
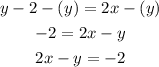
The answer is:
