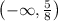Question

I am having trouble with this equation & how to correctly use the [ & ) when it comes to writing in interval notation.

Answer 1

We need to solve the inequality:

`4\left(2-x\right)>\left(5x-7\right)-\left(x-10\right)`

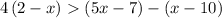
In order to do so, we can expand the expressions on each side, then apply the same operations on both sides of the inequality until we isolate the variable x and find the solution.

By expanding the expression, we obtain:

`\begin{gathered} 4(2)+4(-x)>5x-7-x-(-10) \\ \\ 8-4x>5x-x-7+10 \\ \\ 8-4x\gt4x+3 \end{gathered}`

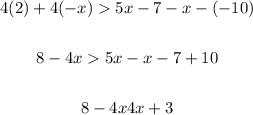
Now, adding 4x to both sides, we obtain:

`\begin{gathered} 8-4x+4x>4x+3+4x \\ \\ 8>8x+3 \end{gathered}`

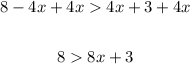
Subtracting 3 from both sides, we obtain:

`\begin{gathered} 8-3>8x+3-3 \\ \\ 5>8x \end{gathered}`

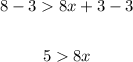
Then, dividing both sides by 8, we obtain:

`\begin{gathered} (5)/(8)>(8x)/(8) \\ \\ (5)/(8)>x \\ \\ x<(5)/(8) \end{gathered}`

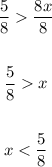
Notice that x must be less than 5/8. Thus, 5/8 does not belong to the solution set. We represent this using (..., ...) for interval notation (open interval). Also, since there is no beginning to the interval solution, we write -∞ in replacement of the left boundary of the set.

Therefore, the solution set is:

Answer

`\left(-\infty,(5)/(8)\right)`