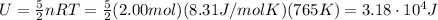The internal energy of an ideal gas is given by:
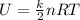
where
k is the number of degrees of freedom of the molecules of the gas
n is the number of moles
R is the gas constant
T is the absolute temperature.
For a diatomic gas, k=5. In our problem, the number of moles is n=2.00 and the absolute temperature of the gas is T=765 K, so its internal energy is