Question

Water at 288.7 k flows through a 15.24-cm. diameter horizontal pipe into a 190-l drum. determine the minimum time it will take to fill the drum if the flow remains laminar.

Answer 1

The flow will be laminar if Reynold's number
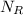`N_(R)` is less than 2000.

Use the Reynold's formula and rearrange to calculate velocity of water in the pipe.

`N_(R) = (v D)/(\\u)`

Where,
`v` is velocity of the fluid,
`D` is the diameter of pipe, and
`\\u` is the kinematic viscosity i.e.
`1.12 * 10^(-6) m^2/s` for water at 288.7 K from Appendix.

So, velocity is:

`v = (N_(R) \\u)/(D)`

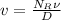
The flow rate Q:

`Q = vA=v\pi D^2/4=((N_R \\u)/(D) \pi D^2)/(4) =[tex] t = (V)/((N_R \\u \pi D)/(4)) = (4V)/(N_R \\u \pi D) =(4 * 190 L(10^(-3) m^3)/(L))/(2000 * 1.12* 10^(-6) m^2/s \pi 15.24 cm(1 m)/(100 cm)) = 2226.3 s (1 min)/(60 s)= 37.1 min` [/tex]

Where A is the area of cross section of pipe.

The time taken to fill is:

`t = Q/V`

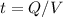
Where V is the capacity of the tank.