Answer:
Using the formula:
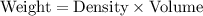
As per the statement:
Given a 10 foot length of tree trunk with a radius of 3 feet.
Volume of tree trunk(V) is given by:
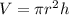
where, r is the radius and h is the length of the tree trunk.
Substitute r = 3 ft and h = 10 ft and use
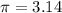
then;
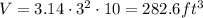
It is also given it has a density of 45 lb/ft^3
then;
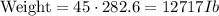
Therefore, the the weight of the tree trunk section is, 12,717 Ib