Explanation:
The function f(x) is defined as a line with a slope of -3 and a y-intercept of 4, hence following the definition of the slope-intercept form of a line,
 .
.
Similarly, for g(x) as shown in the graph. First, to find the slope of the line defined by g(x),
 .
.
Moreover, it is given that the line passes through the point (0, 7) which is the y-intercept of g(x). Thus,

It is known that all polynomial functions are defined everywhere along the real number line and since both functions, f and g, are polynomial functions of the 1st degree, represented by the general form of the function

where
 is the slope of the line and
is the slope of the line and
 is the y-intercept (the y-coordinate of the point in which the line intersects the y-axis) of the linear function with their domains following the set
is the y-intercept (the y-coordinate of the point in which the line intersects the y-axis) of the linear function with their domains following the set
 .
.
Furthermore, both functions f and g have no points of discontinuity (no points where the function is not defined). Hence, the range of functions f and g is
 .
.
It is shown above that when the slope of
 and
and
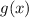 are compared, the following inequality describes the relationship.
are compared, the following inequality describes the relationship.

whereas the comparison of the y-intercept,
 , of both functions is explained by the inequality
, of both functions is explained by the inequality
