Answer:
The limit of the function does not exist.
Explanation:
If
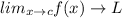 , then L is the limit of the function at x=c.
, then L is the limit of the function at x=c.
The limit of a function exist if left hand limit at a point is equal to the right hand limit at that point.
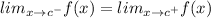
From the given graph it is clear that the left hand limit of the function is

The right hand limit of the function is
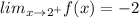
Since
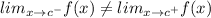 , therefore the limit of the function does not exist.
, therefore the limit of the function does not exist.