Question

Q6 Q12.) Which of the following four statements establishes the​ identity?

Answer 1

tan^2t / sint = tant*tant*1/sint
=tant*sint/cost*1/sint
=tant*1/cost
=tant*sect

so A is the correct ans...not D :)

Answer 2

Comment
Usually it is best to work on one side exclusively and then go to the other if need be.

Left Hand Side
Reduce everything down to Sines and Cosines.
Tan^2(t)
======
Sin(t)
Use Tan(t) = Sin(t) / Cos(t) to reduce this further.

Sin^2(t)
---------
Cos^2(t)
=======
Sin(t)
------
1
Notice I put a 1 underneath the Sin(t). I did this so we could use the rule for a fraction divided by a different fraction.

The rule for this kind of division is turn the denominator upside down and multiply.

It will look like this


`(Sin^2(t))/(Cos^2(t)) * (1)/(sin(t))`

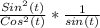
Now cancel one of the sin(t)s. You get
sin(t)
====
cos^2(t)

You are almost done. Sin(t)/cos(t) = tan(t) You have 1 cos(t) left over in the denominator.

Tan(t)
====
Cos(t)

Now to make it clearer, you could write this as
Tan(t) * 1
=======
cos(t)

1/ cos(t) = sec(t). Your final answer on the left is

Tan(t) * sec(t)

That's exactly what is on the right. You are done with the left hand side.

but matching that with your answers has to be the last step.
B and D both have the definition for the Cot(t) not the Tan(t). They are both incorrect.

A is incorrect because 1/sin(t) = csc(t)

Note that C is not precisely correct, because it should be tan(t) * sec(t). Latex can do that to you. I'm picking C, but if that's not correct, let me know and I'll reopen this to edit it.

C<<<<<answer.