Question

Write the quadratic equation in factored form. Be sure to write the entire equation.

x 2 + x - 12 = 0

Answer 1

so this answer to this equation i got this:

x^2+x-12=0
x^2+4x-3x-12=0
x(x+4)-3(x+4)=0
(x-3)(x+4)=0

so (x-3)(x+4)=0 should be the answer

Hope this helped :)
Have a great day

Answer 2

`(x+4)(x-3)=0`

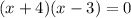
Explanation:

A general expanded form of a quadratic equation could be write as follws:

`ax^(2) +bx+c=0`

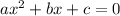
On the other hand, factored form equation could be generally write as:

`(x+q)(x+p)`

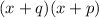
Where the parameters q and p are called the roots of the function.

1. In the case
`x^(2) +x-12=0`, and taking into account the above, a = 1, b = 1 and c = - 12; and we need to find q an p.

2. Form the two factors taking into account the operation signs.

`(x+ p)(x-q)=0`

Note that in the first factor the sign of p is '+' because of the multiplication between the sign 'a (+)' and 'b (+)', then
`+ * + = +`.

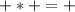In the same way, for the second factor the sign of q is '-' becasuse of the multiplication between the sign of 'b (+)' and 'c (-)', then
`+ * - = -`.

3. As a=1, if you want to write a factored form you only need to find two numbers (p and q) whose multiplication is equal to -12, and whose sum is equal to +1.

By trial and error method you could determine that p=4 and q =-3 due to:

`p*q=12\\(4)*(-3)=12\\p+q=1\\(4)+(-3)=1\\`

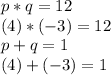
4. Locate the results of p and q in the two factors form:

`(x+ p)(x-q)=0\\(x+4)(x-3)=0`

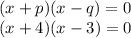
This is the factored form of the quadratic equation
`x^(2) +x-12=0`