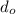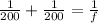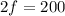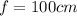Answer:
B. 100 cm
Step-by-step explanation:
Using mirror equation;
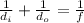
(Please ignore the A cap, I don't know how it appeared here, It's not in the equation tool )
where
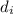 is distance of image = 200 cm
is distance of image = 200 cm
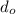 is distance of object = 200 cm
is distance of object = 200 cm
and
 is focal point.
is focal point.
.......substituting for
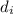 and
and