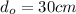Question

Suppose a convex mirror has a focal length of 120 cm. A candle sits directly in front of the mirror. If the image of that candle appears to be 24 cm behind the mirror, how far is the candle from the surface of the mirror?

A. 30 cm
B. 36 cm
C. 150 cm
D. 600 cm

Answer 1

We can solve the problem by using the mirror equation:

`(1)/(f) = (1)/(d_o)+ (1)/(d_i)`
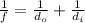
where
f is the focal length

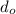
`d_o` is the distance of the object from the mirror

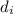
`d_i` is the distance of the image from the mirror

For the sign convention, the focal length is taken as negative for a convex mirror:

`f=-120 cm`
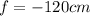
and the image is behind the mirror, so virtual, therefore its sign is negative as well:

`d_i=-24 cm`
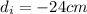
putting the numbers in the mirror equation, we find the distance of the object from the mirror surface:

`(1)/(d_o) = (1)/(f)- (1)/(d_i)= (1)/(-120 cm) - (1)/(-24 cm)= (1)/(30 cm)`
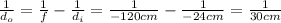
So, the distance of the object from the mirror is
`d_o = 30 cm`