Answer:
It will not make it outside the hole
Step-by-step explanation:
It is given that,
Mark is in a deep hole looking for treasure. He is standing 18 feet below the surface. He throws an old ring he found with an initial upward velocity of 33 ft/sec.
Using the formula,
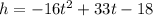 ........(1)
........(1)
Where
h is the height of the ring in feet, t is in seconds since Mark threw it.
On solving quadratic equation (1) as :
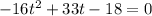
Using the relation :
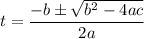
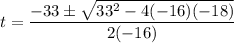
The solution (time) of above equation is complex. So, the correct option is (D) " It will not make it outside the hole"